前段时间公司接了starkware的审计项目,对其零知识证明实现进行深入的检查。坦白说,这方面的理解非常困难,因为我自己本身密码学的基础比较薄弱,而且项目目前没有结合实际的区块链背景,代码实现还是在数学层面,所以其中困难可想而知。具体发现的问题这里不提,公司的公众号上应该会发,这里我介绍下zk-stark的算法,重点参考的文献就是他们的online-course和medium文章。链接如下。
https://starkware.co/stark101-onlinecourse/
https://medium.com/starkware
概述
先简单讲下stark协议整体概述吧。协议中有prover和verifier两个角色。prover要向verifier证明自己知道某个解。 首先,我们拿到一个问题,叫做statement。通过数学手段将这个statement转为多项式,将对这个statement的证明转为对多项式的证明。 这个证明其实是证明这个多项式的阶小于某个值。prover会把这个多项式扩展到一个较大的域上,计算域上取的所有点的一个默克尔树的根, 然后prover在最后证明的过程中,verifier在多项式上取几个点(这么说可能数学上不大精确),这个取点的过程必须是随机的。取出的点给prover。prover通过返回这些点的邻居点就能让verifier计算出默克尔树的根。如果这个根和那个先前发过去的根一样,那么就认为是证明成功了。详述
这里具体的过程我们就用stark oneline course的ppt来做一些讲解。LDE(low degree extension)
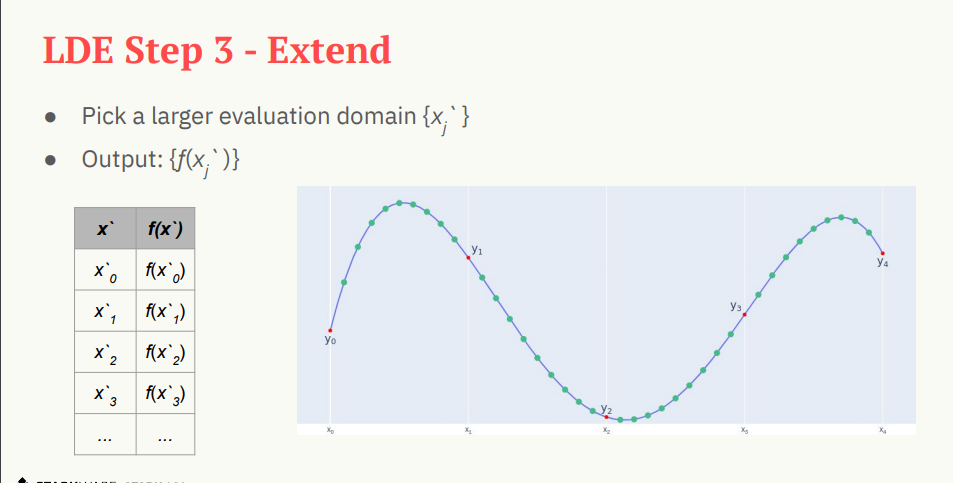
用这张图做例子吧。存在一个数列,这个数列的第1000项是100,且每项之间有已知的规律,也就是说,我们知道了第一和二项就能一直往后算。Prover要证明的是,自己知道这个第一二项,使得第1000项是100。于是乎,prover就拿出一些点,这些点都满足这个数列的规律。可以理解是上面的红点。然后,数学部分就来了,通过一个快速傅里叶变换出现这些同样满足规律,在更大域上的绿点。
Commitment

事实上,我们要证明的那个数列,满足一定的规律,这些规律可以组合成Compositional Polynomial,我的理解是上面那个CP是通过限制和Trace生成的。生成以后,就是通过它的Fri协议消除阶数。因为实际上的那个trace或者说CP这一层很大,把他的阶数往下消除后,计算每一层的Root,发给verifier。看下源码的话,感觉这里就是把变量x变成x^2实现这个效果。Prover这边会将生成的每一层的Merkle root发送给verifier。
Decommitment

在Decommitment阶段,verifier随机选点,例如这里选了cp0(x),那个prover就会把这个点到root的路径上的邻居节点发到verifier那边。通过这些点,verifier就可以计算出每一层的root了。进而和最初prover发过来的比较就能判断真伪。
而实际上,这个过程是交互的,每一层verifier都要选点,但是实现者希望这个过程不是交互的,就用了Fiat–Shamir heuristic将这个过程转为非交互的,简单来说就是通过一个哈希和最初的一个种子来选点。
https://en.wikipedia.org/wiki/Fiat%E2%80%93Shamir_heuristic
大致的过程就如上,实际上代码和理论在审计完成后我也有许多的不解,甚至于开始理解的现在回忆都有些迷糊了。密码学果然还是太难了。